首先将坐标系$\{B\}$和一个已知参考坐标系$\{A\}$重合。将$\{B\}$绕矢量$^A\hat{K}$按右手定则旋转$\theta$角度。

等效旋转矩阵的表示形式推导：

目标：将向量$v=(x,y,z)$绕一般方向（而不是主轴方向）$\hat{r}$（假设$\hat{r}$是单位向量，如果不是，单位化）旋转$\theta$角度，如下图：

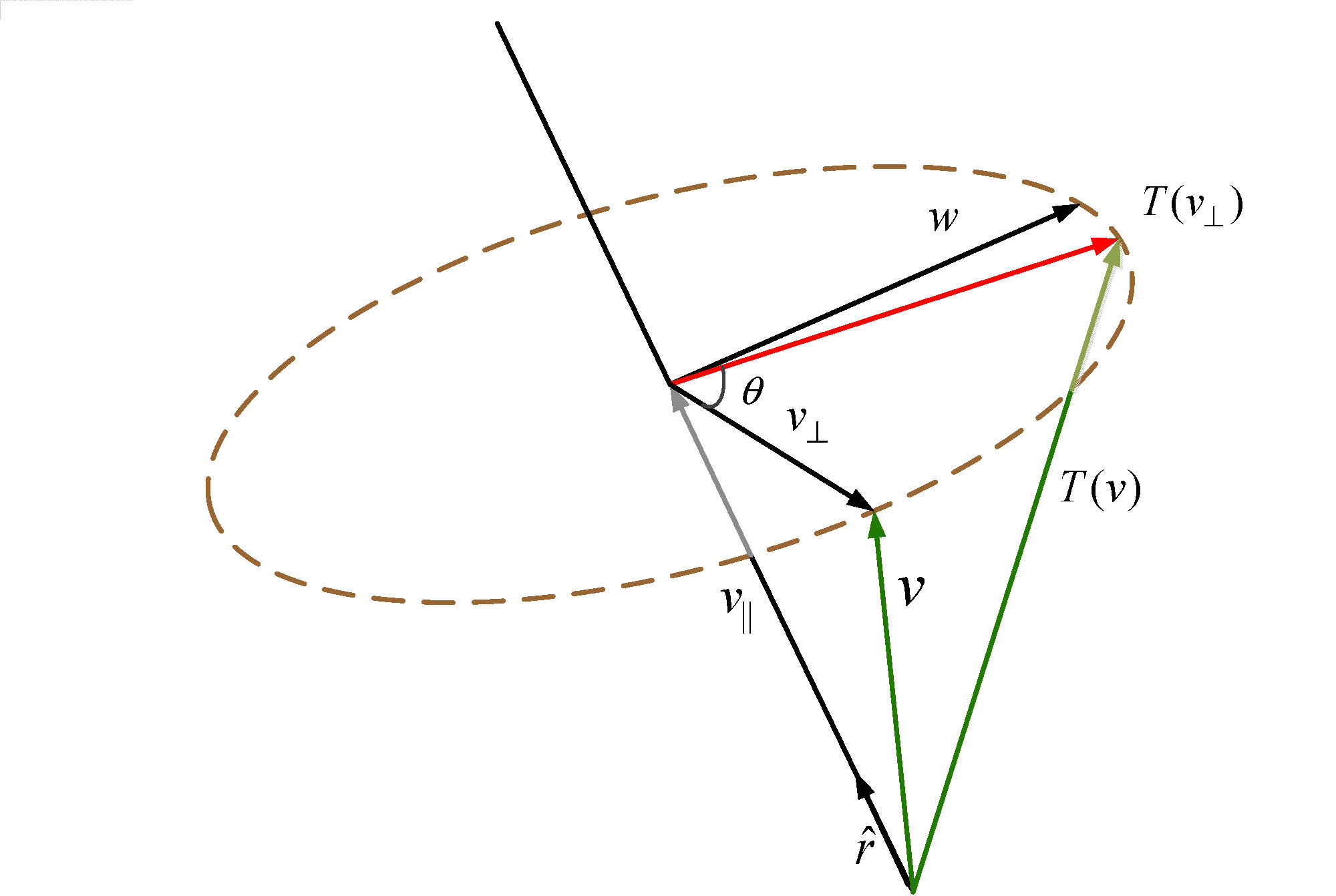
首先，将向量$v$分解为两部分：平行于$\hat{r}$的$v_{||}$和垂直于$\hat{r}$的$v_{\bot}$，并且很容易可以得到:

\[v_{||}=(v\cdot \hat{r})\hat{r}\]

\[v=v_{||}+v_{\bot}\]

\[v_{\bot}=v-v_{||}\]

\[v_{\bot}=v-(v\cdot \hat{r})\hat{r}\]

假设，$T$是我们所要研究的旋转，我们需要计算$T(v)$：

\[\begin{align}T(v)&=T(v_{||}+v_{\bot})\\
&=T(v_{||})+T(v_{\bot})\end{align}\]

因为$v_{||}$平行于旋转轴$\hat{r}$，所以

\[T(v_{||})=v_{||}\]

可以得到：

\[T(v)=v_{||}+T(v_{\bot})\]

其中，$T(v_{\bot})$是唯一需要求解的量。所以我们建立旋转平面上的两个基向量(如下图)，把$v_{\bot}$作为第一个基向量，第二个基向量用

\[\begin{align}w&=\hat{r}\times v_{\bot}\\&=\hat{r}\times v \end{align}\]

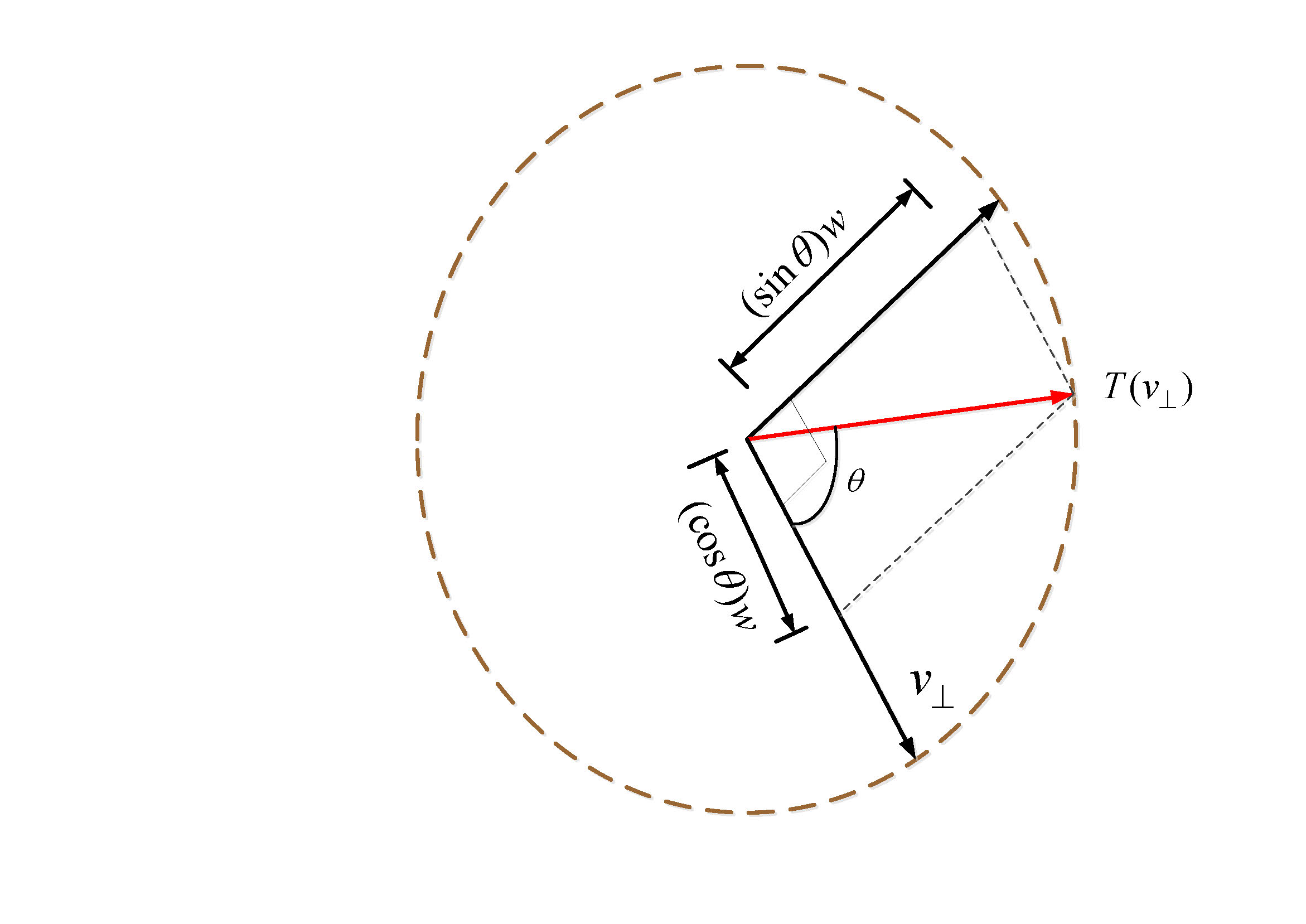
根据上图，我们可以得到：

\[\begin{align} T(v_{\bot})&= v_{\bot}cos\theta+ w sin\theta\\&= v_{\bot}cos\theta+ (\hat{r}\times v)sin\theta\end{align}\]

因此，

\[\begin{align}T(v)&=v_{||}+T(v_{\bot})\\
&=(v\cdot \hat{r})\hat{r}+ v_{\bot}cos\theta+ (\hat{r}\times v)sin\theta\\
&=(v\cdot \hat{r})\hat{r}+ [v-(v\cdot \hat{r})\hat{r}]cos\theta+(\hat{r}\times v)sin\theta\\
&=(v\cdot \hat{r})\hat{r}+ vcos\theta- (v\cdot \hat{r})\hat{r}cos\theta+ (\hat{r}\times v)sin\theta\\
&=(1-cos \theta)(v\cdot \hat{r})\hat{r}+ v cos\theta+ (\hat{r}\times v)sin\theta\end{align}\]

-------------------------------------------------------------

得到的该式为Rodrigues公式：

\[T(v)=(1-cos \theta)(v\cdot \hat{r})\hat{r}+ v cos\theta+ (\hat{r}\times v)sin\theta\]

-------------------------------------------------------------

至此，经过变换之后的向量形式已经表示出来了。可以分别通过三个基向量来求得等效旋转矩阵的一般形式：

\[p=\begin{vmatrix}1 &0 &0\end{vmatrix}^T \]

将向量$p$绕轴$\hat{r}=[k_x,k_y,k_z]$旋转(这里为了和参考书形式相同，采用$k$表示)之后的形式表示为，

\[\begin{align}
p'&=(1-cos \theta)(p\cdot \hat{r})\hat{r}+ pcos\theta+(\hat{r}\times p)sin\theta\\
&=(1-cos\theta)\left[\left(\begin{matrix}1\\0\\0\end{matrix}\right)\cdot \left(\begin{matrix}k_x\\k_y\\k_z\end{matrix}\right)\right]\left(\begin{matrix}k_x\\k_y\\k_z\end{matrix}\right)+\left(\begin{matrix}1\\0\\0\end{matrix}\right)cos\theta + \left[\left(\begin{matrix}k_x\\k_y\\k_z\end{matrix}\right)\times \left(\begin{matrix}1\\0\\0\end{matrix}\right)\right]sin\theta\\
&=\left[\begin{matrix}k_x^2(1-cos\theta)+cos\theta\\k_xk_y(1-cos\theta)+k_zsin\theta\\k_xk_z(1-cos\theta)-k_ysin\theta\end{matrix}\right]\end{align}\]

类似的，可以将$q=\begin{vmatrix}0 &1 &0\end{vmatrix}^T$，$r=\begin{vmatrix}0 &0 &1\end{vmatrix}^T$经过旋转之后的形式表示为：

\[q'=\left[\begin{matrix}k_xk_y(1-cos\theta)-k_z sin\theta\\k_y^2(1-cos\theta)+cos\theta\\k_yk_z(1-cos\theta)+k_xsin\theta\end{matrix}\right]\]

\[r'=\left[\begin{matrix}k_xk_z(1-cos\theta)+k_y sin\theta\\k_yk_z(1-cos\theta)-k_xsin\theta\\k_z^2(1-cos\theta)+cos\theta\end{matrix}\right]\]

最后，可以得到等效旋转阵的形式：

\[R_r(\theta)=\left[\begin{matrix}k_x^2v\theta+c\theta&k_xk_yv\theta-k_zs\theta&k_xk_zv\theta+k_ys\theta\\k_xk_yv\theta+k_zs\theta&k_y^2v\theta+c\theta&k_yk_zv\theta-k_xs\theta\\k_xk_zv\theta-k_ys\theta&k_yk_zv\theta+k_xs\theta&k_z^2v\theta+c\theta\end{matrix}\right]\]

其中，$c\theta=cos\theta$,$s\theta=sin\theta$,$v\theta=1-cos\theta$，$\theta$是由右手定则确定的，即大拇指指向$\hat{r}$的正方向。